(from Greek poly- meaning "many" and -edron meaning "face").
Each face is a polygon (a flat shape with straight sides).
Cuando hablamos de figura geométrica, lo hacemos en dos dimensiones (2D): largo y ancho, pero cuando hablamos de un cuerpo geométrico lo hacemos en tres dimensiones (3D) largo, ancho y alto.
Es así como dejamos de hablar de una geometría plana, para
introducirnos en el estudio de una geometría espacial. En la figura
podemos observar, gráficamente, la diferencia entre ambos objetos
matemáticos.
Los poliedros se relacionan
estrechamente con las figuras planas, ya que un cuerpo geométrico está
compuesto por caras que tienen forma de figuras planas o polígonos, como
normalmente las conocemos. Es así entonces que definimos a los
poliedros de la siguiente manera: Un poliedro es la región del espacio
delimitada por polígonos. Lo poliedros o sólidos geométricos son figuras
en tres dimensiones que poseen dos propiedades: el área de la
superficie y el volumen. Los cuerpos geométricos se dividen en cuerpos
redondos y poliedros.
Podemos reconocer una anatomía de los poliedros así:
- Cara: cada uno de los polígonos que forman el poliedro
- Aristas: Línea que se forma donde se unen dos caras
- Vértices: Punto donde se cortan tres aristas.
- Ángulos diedros: Ángulo formado por dos caras que tienen una arista en común.
- Ángulo poliedro: Ángulo formado por tres o más caras que tienen un vértice en común.
- Diagonal: Recta que une dos vértices de caras diferentes
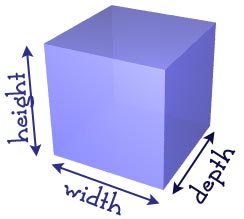
Three Dimensions
It is called three-dimensional, or 3D because there are three dimensions: width, depth and height
Quedan por nombrar otros elementos que se
irán estudiando con el paso del tiempo y que tienen que ver con algunas
condiciones particulares de cada grupo de cuerpos geométricos.
Miremos ahora una breve clasificación de
poliedros. Empecemos por los más estudiados que son los poliedros
regulares o sólidos platónicos, recordemos que se llaman así porque
todas sus caras son polígonos regulares.
Los primas y pirámides reciben sus nombres según la forma poligonal de sus bases, miremos algunas de ellas
Luego de mirar los anteriores cuerpo
geométricos observemos un poco sobre qué es o qué son los cuerpos
redondos. Estos son sólidos limitados por regiones curvas o planas y
curvas, es decir, son aquellos que tienen al menos una de sus caras de
forma curva; también se llaman cuerpos de revolución porque pueden
obtener a partir de una figura alrededor de un eje.
Counting Faces, Vertices and Edges
When we count the number of faces (the flat surfaces), vertices (corner points), and edges of a polyhedron we discover an interesting thing:
The number of faces plus the number of vertices
minus the number of edges equals 2
This can be written neatly as a little equation:minus the number of edges equals 2
F + V − E = 2
It is known as Euler's Formula (or the "Polyhedral Formula") and is very useful to make sure we have counted correctly!
Let's try some examples:
This cube has:
|
 |
| F + V − E = 6 + 8 − 12 = 2 | |
This prism has:
|
 |
| F + V − E = 5 + 6 − 9 = 2 | |
Otra clase de sólidos de importancia son los llamados Arquimedianos o sólidos truncados, estos cuerpos son el resultado de un truncamiento o corte transversal en los vértices de los sólidos platónicos, existen dos tipos de corte: a un tercio o a un medio. Miremos algunos de ellos.
Para terminar es recomendable que veamos el siguiente video que nos permitirá entender, un poco más a fondo, sobre qué son los poliedros y los cuerpos redondos.
Todos los videos, aplicaciones e imágenes pertenecen a sus autores, en este sitio web se usarán, respetando la autoría de ellos y con fines meramente educativos, no lucrativ






